1. Qué nos enseña la primera ley de Newton?
2. Qué nos enseña la segunda ley de Newton?
3. Cómo debe entenderse el concepto de partícula en este curso de física mecánica?
4. Qué significa el hecho de que un cuerpo este acelerado?
5. La segunda ley de Newton se fundamenta en dos conceptos fundamentales, cuáles son?
6. Cuales es el modelo matemático que identifica la segunda ley de Newton?
7. ΣF = ma da lugar a la aplicación de la segunda ley de Newton en forma escalar según sea la trayectoria del cuerpo. Cuáles son estas ecuaciones escalares?
8. Qué nos enseña la Tercera ley de Newton?
9. Qué es un diagrama de cuerpo libre?
10. Cuándo se presenta y como se representa una fuerza Normal?
11. Qué son las fuerzas de rozamiento?
12. Qué es La Fuerza de rozamiento Estática máxima fs?
13. Qué es la Fuerza de rozamiento Cinética o Dinámica fk?
14. Qué es la cinética o dinámica?
15. Cuál es el modelo matemático para la fuerza de rozamiento estático máxima fs.
16. Cuál es el modelo matemático para la fuerza de rozamiento dinámica o cinético fk.
17. Entre que valores se encuentran los coeficientes de rozamiento estático y cinético μs y μs?
18. Cómo se consideran las cuerdas en el análisis de los ejercicios en este curso de física mecánica?
19. Cómo se consideran las poleas en el análisis de los ejercicios en este curso de física mecánica?
20. Cuáles son las unidades para el coeficiente de rozamiento μ?
1. Para la figura la fuerza F=50 N , M=10 Kg , el ángulo θ=30° . Determine el valor del coeficiente de rozamiento estático necesario para que el sistema permanezca en reposo y el valor de la tensión.
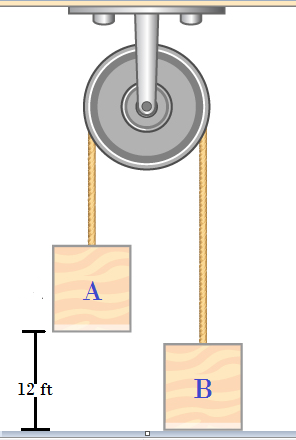
2. En la figura el bloque A=20 Lb , el bloque B=10 Lb . El sistema se libera del reposo. Determine la aceleración de cada bloque, la velocidad con la que el bloque A choca el suelo y la altura maxima a la que sube el bloque B .
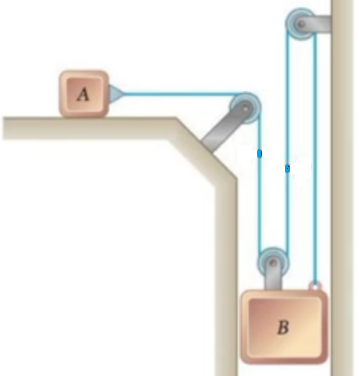
3. En la figura el boque A es de 8 Lb , el bloque B es de 16 Lb , el coeficiente de rozamiento cinético uk=0.1 . Determine la aceleración de cada bloque y el cambio de posición del bloque B pasados 2 s si el sistema se libera desde el reposo.
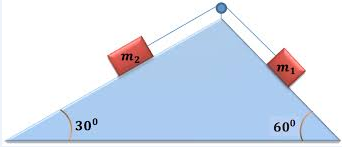
4. En la figura el boque m1 es de 10 Kg , el bloque m2 es de 20 Kg , el coeficiente de rozamiento cinético uk=0.05 . Determine la aceleración de cada bloque y la tensión en la cuerda.
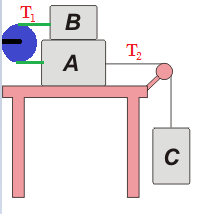
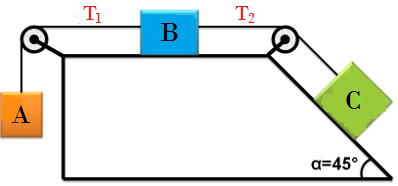
5. El coeficiente de rozamiento cinético entre todas las superficies horizontales es de 0.1 , la masa de los bloques son ma=8 Kg mB=4 Kg mC=12 Kg . Determine la aceleración de cada bloque y las tensiones en las cuerdas.
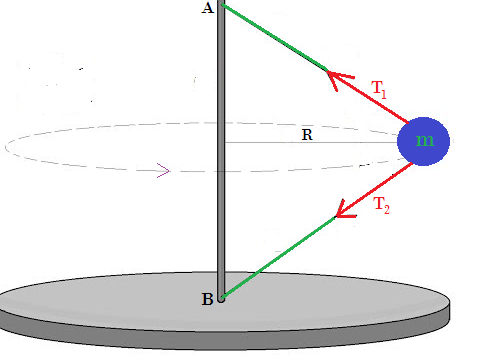
6. La estera de 8 Kg gira horizontalmente al rededor de una varilla vertical de longitud 6 m a una rapidez de 20sm . La esfera esta atada a 2 cuerdas de longitud 5 m cada una. Determine la magnitud de la aceleración normal, de la aceleración tangencial, de la aceleración total y las tensiones en las cuerdas.
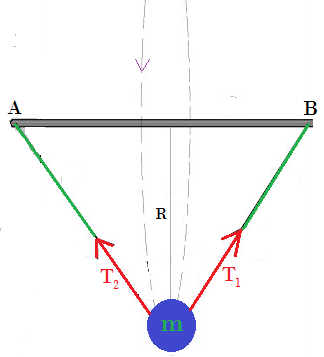
7. La estera de 8 Kg gira verticalmente alrededor de una varilla horizontal de longitud 6 m a una rapidez de 20sm . La esfera esta atada a 2 cuerdas de longitud 5 m cada una. Determine la magnitud de la aceleración normal, de la aceleración tangencial, de la aceleración total. Determine la tensión en cada cuerda en el punto mas bajo de la trayectoria y en el punto más alto de la trayectoria.
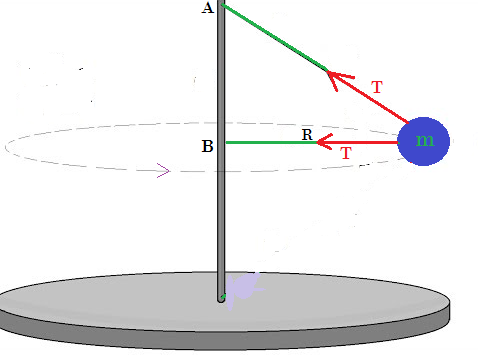
8. La esfera de 6 slug se puede mover libremente por la cuerda atada en los puntos A y B de la varilla. Cuando la varilla comienza a girar, la esfera sube y llega hasta la posición mostrada (la sección de cuerda desde el punto B hasta donde está la masa se pone horizontal) y en ese instante la masa gira con rapidez constante. Determine la rapidez requerida para que la esfera gire en estas condiciones. Determine su aceleración normal.
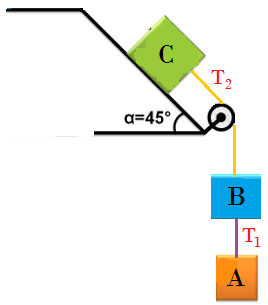
9. En la figura el bloque A es de 10 Lb , el bloque B es de 8 Lb , el bloque C es de 4 Lb , la aceleración del sistema es de 2s2ft . Determine el valor del coeficiente de rozamiento cinético y el valor de las tensiones en las cuerdas.
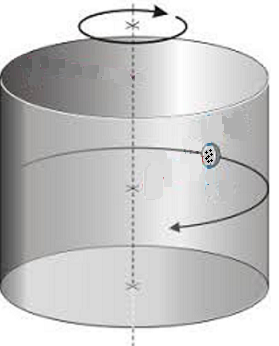
10. El cilindro de acero vertical de diámetro 4 m gira alrededor de su eje tan rapido que hace que una placa circular de cobre de 80 Kg que se encuentra en su interior se mantenga contra la pared del cilindro tal como se muestra en la figura. Determine la rapidez con la que debe girar el cilindro para que la placa no resbale. Determine la fuerza que ejerce el cilindro sobre la placa.
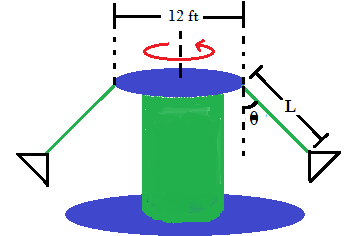
11. En la atracción mecánica las sillas voladoras se desplazan a 25.93sft . El diámetro de la plataforma giratoria es de 12 ft . Determine el ángulo θ y la longitud L de la cuerda que sujeta cada silla.
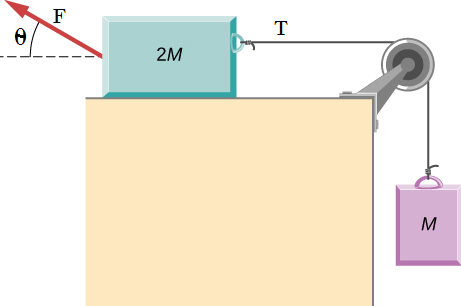
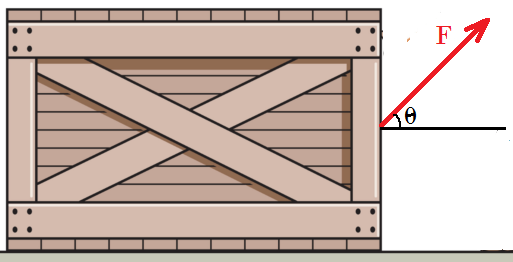
12. La caja de 10 Slug estando en reposo se le aplica una fuerza de 120 Lb formando un ángulo de θ=45° como se muestra en la figura. El coeficiente de rozamiento cinético entre la caja y la superficie es de 0.15 . Determine la velocidad y el cambio de posición de la caja pasados 4 s de haberse puesto en movimiento.
13. Un automóvil de 500 Kg se desplaza por una curva de radio 20 m y peralte de 36.87° . El coeficiente de rozamiento estatico entre la pista y las llantas del vehículo es de 0.2 . Determine la máxima rapidez constante que debe tener el automóvil para que no derrape hacia arriba del peralte. Determine la fuerza que ejerce la pista sobre el automóvil.

14. Determine la rapidez mínima requerida para que el automóvil del ejercicio anterior no derrape hacia abajo del peralte de la pista. Determine la fuerza que ejerce la pista sobre el automóvil.
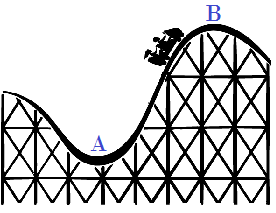
15. El carro de la montaña rusa junto con los pasajeros tiene 150 Slug . El carro tiene una rapidez de 40sft cuando pasa por el punto A que tiene un radio de curvatura de 15 ft . El punto B tiene un radio de curvatura de 5 ft . Determine la fuerza ejercida por la pista sobre el carro cuando pasa por el punto A . Determine la velocidad máxima que puede tener el carro al pasar el punto B y mantenerse aún sobre la pista.
16. El sistema muestra el elevador E de 500 Kg , el contrapeso B de 150 Kg . Si se aplica una fuerza de 2500 N a la cuerda en el punto A , determine la velocidad del elevador 2 segundos luego activar el sistema desde el reposo.
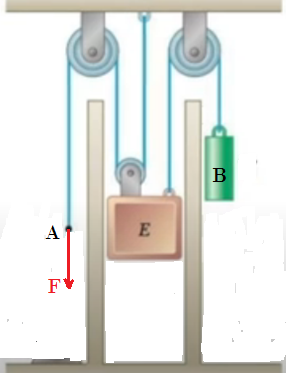
17. En la gráfica del ejercicio anterior, el sistema muestra el elevador E de 120 Lb , el contrapeso B de 40 Lb . Si se aplica una fuerza de 50 Lb a la cuerda en el punto A , determine la aceleración del punto P y el cambio de posición del punto P de la cuerda 2 segundos luego activar el sistema desde el reposo.
18. El automóvil de carreras gira sobre la curva de radio 200 m con peralte a 40sm . Determine el ángulo θ que debe tener el peralte para que las ruedas del automóvil no dependan de la fricción para evitar que el automóvil derrape sobre la curva.

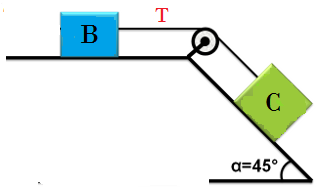
19. Determine la aceleración del sistema y la tensión en la cuerda si el bloque B es de 100 Kg , el bloque C es de 50 Kg y el coeficiente de rozamiento cinético entre los bloques y las superficies es de 0.2
20. Determine la aceleración y la tensión T1 (entre los bloques A y B ) en el sistema mostrado, si el bloque C es de 100 Kg , el bloque B es de 100 Kg , el bloque A es de 50 Kg y el coeficiente de rozamiento cinético entre el bloque C y la superficie es de 0.2 .